Пт, 10/04/2009 - 13:01 — Анастасия
Часть 2
Задание 17
Постройте график функции Укажите наименьшее значение этой функции.
Укажите наименьшее значение этой функции.
Ответ: график изображен на рисунке; унаим. = –3.
Решение. График — парабола, ветви которой направлены вверх. Найдем координаты вершины:

(В решении должны быть вычислены координаты еще нескольких точек, в том числе точки пересечения параболы с осью у.) Наименьшее значение функции равно –3.
Замечание. Учащийся может вычислить координаты вершины параболы и другим способом.
Комментарий. В случае отсутствия вычислений в чистовике при правильном построении параболы решение должно быть засчитано.
Задание 18
Выясните, имеет ли корни уравнение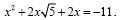
Ответ: не имеет.
Решение. Представим уравнение в виде: Определим знак дискриминанта:
Определим знак дискриминанта:  Так как
Так как  , то уравнение корней не имеет.
, то уравнение корней не имеет.
Замечание. Уравнение может быть представлено в виде: ; учащийся может вычислить дискриминант D квадратного уравнения.
; учащийся может вычислить дискриминант D квадратного уравнения.
Комментарий. Ошибки в составлении выражения D1 (или D), в применении формулы квадрата двучлена считаются существенными, и решение при их наличии не засчитывается.
Задание 19
Найдите сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4.
Ответ: 9600.
Решение. Пусть S — искомая сумма; S = S1−S2, где S1 — сумма всех натуральных чисел, не превосходящих 160, S2 – сумма всех натуральных чисел, кратных 4 и не превосходящих 160.
Найдем S1: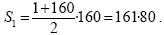 В последовательности (an) чисел, кратных 4 и не превосходящих 160, a1 = 4, an = 160. Найдем число членов этой последовательности. Так как она задается формулой an = 4n, то 4n = 160 , n = 40.
В последовательности (an) чисел, кратных 4 и не превосходящих 160, a1 = 4, an = 160. Найдем число членов этой последовательности. Так как она задается формулой an = 4n, то 4n = 160 , n = 40.
Теперь найдем
Получим: S = S1−S2= 161*80 − 82*40 = 40(322−82) = 9600.
Задание 20
Найдите наименьшее значение выражения (2x+y+3)2 + (3x−2y+8)2 и значения x и y , при которых оно достигается.
Ответ: наименьшее значение выражения равно 0, оно достигается при x = −2, y =1.
Решение. При любых значениях х и у (2x+y+3)2 + (3x−2y+8)2 > 0. Значение, равное 0, достигается только в том случае, когда 2x+ y +3 и 3x−2y+8 равны нулю одновременно.
Составим систему уравнений Решив ее, получим: x = −2, y = 1. Таким образом, наименьшее значение выражения равно 0, оно достигается при x = −2, y = 1.
Решив ее, получим: x = −2, y = 1. Таким образом, наименьшее значение выражения равно 0, оно достигается при x = −2, y = 1.
Задание 21
Найдите все значения k, при которых прямая y=kx пересекает в трех различных точках ломаную, заданную условиями:
Ответ: 2/3 < k < 2. Другие возможные формы ответа:
Решение. Построим ломаную, заданную условиями:
Прямая y=kx пересекает в трех различных точках эту ломаную, если ее угловой коэффициент больше углового коэффициента прямой, проходящей через точку (−3;−2), и меньше углового коэффициента прямой, параллельной прямым y =2x−8 и y=2x+4. Найдем угловой коэффициент прямой, проходящей через точку (−3;−2): −2 = −3k , k = 2/3. Угловой коэффициент k прямой, параллельной прямой y=2x−8, равен 2. Прямая y=kx имеет с ломаной три общие точки при 2/3 < k < 2.
Комментарий. Если график построен неправильно, или график построен правильно, но дальнейшие шаги отсутствуют, то решение не засчитывается.
Ответы на тесты ГИА по алгебре (2009 г.).
Часть 1
|
Номер задания
|
Ответ
|
| 1 | 2 |
| 2 | 3 |
| 3 | 2 |
| 4 | – 1,6 |
| 5 | 3 |
| 6 | 4 |
| 7 | 4 |
| 8 | 0,012 |
| 9 | – 2,5 |
| 10 | А(2; 4) |
| 11 | 4 |
| 12 | 3 |
| 13 | 2 |
| 14 | 243 |
| 15 | 3 |
| 16 | 800 тыс. |
Часть 2
Задание 17
Постройте график функции
Ответ: график изображен на рисунке; унаим. = –3.
Решение. График — парабола, ветви которой направлены вверх. Найдем координаты вершины:

(В решении должны быть вычислены координаты еще нескольких точек, в том числе точки пересечения параболы с осью у.) Наименьшее значение функции равно –3.
Замечание. Учащийся может вычислить координаты вершины параболы и другим способом.
Комментарий. В случае отсутствия вычислений в чистовике при правильном построении параболы решение должно быть засчитано.
Задание 18
Выясните, имеет ли корни уравнение
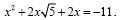
Ответ: не имеет.
Решение. Представим уравнение в виде:
Замечание. Уравнение может быть представлено в виде:
Комментарий. Ошибки в составлении выражения D1 (или D), в применении формулы квадрата двучлена считаются существенными, и решение при их наличии не засчитывается.
Задание 19
Найдите сумму всех натуральных чисел, не превосходящих 160, которые не делятся на 4.
Ответ: 9600.
Решение. Пусть S — искомая сумма; S = S1−S2, где S1 — сумма всех натуральных чисел, не превосходящих 160, S2 – сумма всех натуральных чисел, кратных 4 и не превосходящих 160.
Найдем S1:
Теперь найдем
Получим: S = S1−S2= 161*80 − 82*40 = 40(322−82) = 9600.
Задание 20
Найдите наименьшее значение выражения (2x+y+3)2 + (3x−2y+8)2 и значения x и y , при которых оно достигается.
Ответ: наименьшее значение выражения равно 0, оно достигается при x = −2, y =1.
Решение. При любых значениях х и у (2x+y+3)2 + (3x−2y+8)2 > 0. Значение, равное 0, достигается только в том случае, когда 2x+ y +3 и 3x−2y+8 равны нулю одновременно.
Составим систему уравнений
Задание 21
Найдите все значения k, при которых прямая y=kx пересекает в трех различных точках ломаную, заданную условиями:

Ответ: 2/3 < k < 2. Другие возможные формы ответа:
Решение. Построим ломаную, заданную условиями:

Прямая y=kx пересекает в трех различных точках эту ломаную, если ее угловой коэффициент больше углового коэффициента прямой, проходящей через точку (−3;−2), и меньше углового коэффициента прямой, параллельной прямым y =2x−8 и y=2x+4. Найдем угловой коэффициент прямой, проходящей через точку (−3;−2): −2 = −3k , k = 2/3. Угловой коэффициент k прямой, параллельной прямой y=2x−8, равен 2. Прямая y=kx имеет с ломаной три общие точки при 2/3 < k < 2.
Комментарий. Если график построен неправильно, или график построен правильно, но дальнейшие шаги отсутствуют, то решение не засчитывается.
- Версия для печати
- 128729 просмотров

