Учимся вместе

Олимпиадные задачи 2 тура с решениями и ответами - 2006 год

6 класс

1. Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого. Найдите уменьшаемое и вычитаемое.
2. Будет ли сумма чисел  1 + 2 + 3 + …..+ 2005 + 2006 + 2007 делиться на 2007? Ответ обоснуйте.
3. Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов. Какое наибольшее число клеток понадобится?
4. На выставку привезли 25 собак. 12 из них большие, 8 – маленькие, остальные средние. Только 10 из участников выставки породистые, остальные – дворняжки. Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?
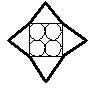
5. Все треугольники, изображенные на рисунке, имеют равные стороны. Радиус каждой из окружностей равен 2 см. Окружности касаются друг друга и сторон квадрата. Чему равен периметр «звездочки», нарисованной жирной линией?

7 класс

1. Восстановите пример: АВС × СВА = 692443.
2. За весну Обломов похудел на 25%, затем за лето поправился на 20%, затем за осень похудел на 10%, а за зиму прибавил 20%. Похудел он в итоге или поправился? Ответ обоснуйте.
3. Какой цифрой оканчивается число 20072006?
4. На клетчатой бумаге со стороной клетки 1 см нарисован треугольник. 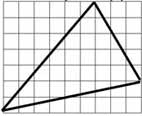Чему равна его площадь?
5. У мамы четыре дочери Поля, Валя, Катя и Маша. Девочки играли и разбили вазу. На вопрос: «Кто это сделал?» Поля, Валя и Катя ответили: «Не я», а Маша – «не знаю». Потом оказалось, что две из них сказали правду, а две неправду. Знает ли Маша, кто разбил вазу? Ответ объясните.

8 класс

1. Решите уравнение x - 6 = |x - 3|/(x - 3).
2. Верно ли равенство 3¹⁰⁰ + 7¹⁰⁰ = 8¹⁰⁰? Ответ обоснуйте.
3. Дворники получают грабли и метлы. Если каждый возьмет одну метлу или одни грабли, то останется 14 метел. А чтобы дать каждому дворнику и одну метлу, и одни грабли, не хватает 10 грабель. Сколько было дворников, сколько метел и сколько грабель?
4. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал туземца узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: «Туземец говорит, что он абориген». Кем был проводник: пришельцем или аборигеном? Ответ обоснуйте.
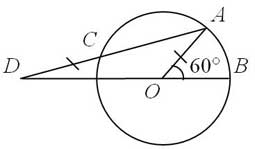
5. В окружности с центром в точке О проведены радиусы ОВ и ОА так, что ﮮАОВ=60°, ОВ = DС. Найдите величину ﮮАDО.

9 класс

1. В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.
2. Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
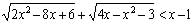
3. Решите неравенство .
4. Решите уравнение x² + 2005x – 2006 = 0.
5. Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?

10 класс 

1. Решите уравнение (x-2)(x-3)(x+4)(x+5) = 1320.
2. На плоскости дан отрезок АВ. Где может быть расположена точка С, чтобы ∆АВС был остроугольным?
3. Найти все натуральные числа, оканчивающиеся на 2006, которые после зачеркивания последних   четырех цифр уменьшаются в целое число раз.
4. Вычислить сумму a²⁰⁰⁶ + 1/a²⁰⁰⁶, если a²– a + 1 = 0.
5. Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей, и т. д. Может ли за некоторое число разрезаний получиться 2006 листка бумаги?

11 класс

1. Докажите, что уравнение  xy = 2006 (x+y) имеет решения в целых числах.
2. Докажите, что если α, β, γ - углы произвольного треугольника, то справедливо тождество cos²α + cos²β + cos²γ + 2 cosα cosβ cosγ = 1.
3. Три шара радиуса R касаются друг друга и плоскости  α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных  шаров. Определите высоту «горки» из четырех шаров.
4. Докажите неравенство x² - 3x³ < 1/6 на луче [1/4; +∞).
5. В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.

Порядок проведения школьного этапа Олимпиады

Рекомендуется подготовка заданий для школьного этапа Олимпиады муниципальными предметно-методическими комиссиями по математике.

Порядок проведения муниципального этапа Олимпиады

Муниципальный этап Олимпиады проводится в один день в ноябре-декабре для учащихся 6-11 классов.
Рекомендуемое время проведения Олимпиады – 4 часа.
Вариант должен содержать 5-6 задач разной сложности. Обязательным является требование включения в вариант заданий по темам, изученным к моменту проведения Олимпиады в соответствии с программами всех базовых учебников по математике. Первые две (самые легкие) задачи варианта должны быть доступны подавляющему большинству участников. Рекомендуется подготовка заданий для муниципального этапа Олимпиады региональными предметно-методическими комиссиями по математике.

Задания школьного и муниципального этапов Олимпиады

Олимпиадные задания школьного и муниципального этапов составляются на основе программ по математике для общеобразовательных учебных учреждений. Также допускается включение задач, тематика которых входит в программы школьных кружков (факультативов). Ниже приводятся только те темы, которые рекомендуется использовать при составлении вариантов заданий текущего учебного года. Важно отметить, что в силу специфики регионов и различий в степени доступности участникам Олимпиады тех или иных источников задач, сложности в составлении (подборе) задач предлагаемой тематики необходимой для данной территории трудности, предметно-методические комиссии могут менять рекомендуемую тематику заданий, сохраняя в целом структуру варианта.
 

К-9. Неравенства