Учимся вместе

Олимпиадные задачи 2 тура с решениями и ответами - 2009 год

 7 класс

1. В данном примере различные цифры зашифрованы различными буквами. Определите, какое равенство зашифровано: ОТВЕТ + ОЧЕНЬ = ПРОСТ.
2. В спортивной секции девочки составляют 60% числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
3. Найти наименьшее шестизначное число, делящееся на 9, все цифры которого различны.
4. Можно ли квадрат со стороной 1 м разрезать на 7 прямоугольников, не обязательно одинаковых, каждый из которых имел бы периметр 2 м?
5. Можно ли покрасить клетчатый квадрат 2009 x 2009 в два цвета – черный и белый (каждая единичная клетка красится одним из этих цветов) – таким образом, чтобы каждая черная клетка имела двух белых соседей, а каждая белая клетка – двух черных соседей (соседями считаем клеточки, которые имеют общую сторону)? Ответ обоснуйте.
   

8 класс

1. Докажите, что 13 + 13² + 13³ + 13⁴ +…+ 13²⁰⁰⁹ + 13²⁰¹⁰ делится нацело на 7.
2. Постройте график функции y = |x - 2| - 2.
3. На сторонах АВ, ВС и АС равностороннего треугольника АВСвзяты соответственно точки D, E, F, так что AD = BE = CF. Каков вид треугольника DEF? Докажите.
4. Известно, что a + b + c = 5, ab + ac + bc = 5. Чему может равняться a² + b² + c²?
5. На 44 деревьях, расположенных по кругу, сидели по веселому чижу. Время от времени какие-то два чижа перелетают на соседнее дерево – один по часовой стрелке, а другой – против. Могут ли все чижи собраться на одном дереве?
   

 Олимпиадные задачи 2 тура с решениями и ответами - 2008 год

2008 год

7 класс

1. Найдите все корни уравнения |х - 2008| = 2009.
2. Гонцу надо было пробежать 24 мили. Две трети этого расстояния он бежал со средней скоростью 8 миль в час. Сможет ли он, увеличив скорость, пробежать остаток пути так, чтобы его средняя скорость на всем пути оказалась равной 12 миль в час.
3. Дима взял 2008 одинаковых квадратиков. Он хочет сложить из всех этих квадратиков прямоугольник. Сколько различных прямоугольников он может получить?
4. Четверо купцов заметили, что если они сложатся без первого, то соберут 90 рублей, без второго – 85, без третьего – 80, без четвертого – 75 рублей. Сколько у кого денег?
5. Последовательность чисел строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на единицу. Например, на втором месте стоит число 14, так как  7² = 49, а 4 + 9 + 1 = 14.  На третьем месте стоит число 17 и так далее. Какое число стоит на 2008-м месте?

8 класс

1. Корень из числа 49 можно извлечь по такой «формуле»: √ 49 = 4 + √9.
2. Существуют ли другие двузначные числа, квадратные корни из которых извлекаются аналогичным образом и являются целыми? Укажите все такие двузначные числа.
3. ABC – равнобедренный треугольник с вершиной А. ﮮА=27°. Точка D симметрична точке В относительно А. Чему равен угол ﮮBCD?
4. Мальчик стоит на автобусной остановке и мёрзнет, а автобуса нет. Ему хочется пройтись до следующей остановки. Мальчик бегает вчетверо медленнее автобуса и может увидеть автобус на расстоянии 2 км. До следующей остановки ровно километр. Имеет ли смысл идти, или есть риск упустить автобус?
5. Про числа aи b известно, что a = b+ 1. Может ли оказаться так, что
   a⁴  =  b⁴?
6. Какое наименьшее количество клеток квадрата 5 x 5 нужно закрасить, чтобы в любом квадрате 3 x 3, являющемся его частью, было ровно
   4 закрашенных клетки?

9 класс

1. Докажите, что число  2008² + 2008² ×  2009² + 2009²  является ли квадратом целого числа.
2. Рассматриваются функции вида y = x² + ax + b, где  а + b = 2008. Докажите, что графики всех таких функций имеют общую точку.
3. На острове рыцарей и лжецов (лжецы всегда лгут, рыцари всегда говорят правду) каждый болеет ровно за одну футбольную команду. В опросе приняли участие все жители острова. На вопрос «Болеете ли Вы за «Спартак»?» ответили «Да» 40% жителей. На аналогичный вопрос про «Зенит» утвердительно ответили 30%, про «Локомотив» - 50%, а про ЦСКА – 0%. Какой процент жителей острова действительно болеет за «Спартак»?
4. В выпуклом пятиугольнике ABCDE  ﮮА = ﮮB =ﮮD = 90°. Найдите ﮮADB, если известно, что в данный пятиугольник можно вписать окружность.
5. Кольцевая дорога поделена столбами на километровые участки, и известно, что количество столбов четно. Один из столбов покрашен в желтый цвет, другой - в синий, а остальные – в белый. Назовем расстояние между столбами длину кратчайшей из двух соединяющих их дуг. Найдите расстояние от синего столба до желтого, если сумма расстояний от синего столба до белых равна 2008 км. 

10 класс

1. Графики функций  у = х² + ах + bи  у = х² + сх + d  пересекаются в точке с координатами  (1; 1).  Сравните  a⁵ + d⁶ и  c⁶- b⁵.
2. Какое наибольшее число ребер шестиугольной призмы может пересечь плоскость, не проходящая через вершины призмы?
3. Решите уравнение : 
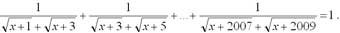4. Докажите, что если стороны треугольника образуют геометрическую прогрессию, то их высоты тоже образуют геометрическую прогрессию.
5. В клетки квадрата 3 × 3 требуется вписать девять различных натуральных чисел так, чтобы все они не превосходили n, и чтобы произведения чисел в каждой строке и каждом столбце были равны. При каком наименьшем n это возможно?

11 класс

1. Найдите такое натуральное число k, что 2008! делится на 2007^k, но не делится на 2008^k. (Напомним, чтоn! = 1·2·3·4·… ·n).
2. Может ли вершина параболы y = 4x² – 4(a + 1)x + a  лежать во второй координатной четверти при каком-нибудь значении а?
3. (a_n) – арифметическая прогрессия с разностью 1. Известно, что S₂₀₀₈ - наименьшая среди всех S_n (меньше суммы первых n членов для любого другого значения n). Какие значения может принимать первый член прогрессии?
4. Внутри равностороннего треугольника со стороной 8 находится равнобедренный треугольник АВС, в котором АС = ВС = 1, ﮮС=120°. Две вершины А и В могут лежать либо на одной стороне большого треугольника, либо на двух. Где при этом может оказаться вершина тупого угла – точка С? Нарисуйте это геометрическое место точек и найдите длину соответствующей линии.
5. Клетчатая прямоугольная сетка m x n связана из веревочек единичной длины. Двое делают ходы по очереди. За один ход можно разрезать (посередине) не разрезанную ранее единичную веревочку. Если не останется ни одного замкнутого веревочного контура, то игрок, сделавший последний ход, считается проигравшим. Кто из игроков победит при правильной игре и как он должен для этого играть?

Олимпиадные задачи 2 тура с решениями и ответами - 2007 год

1. Если Коля купит 11 тетрадей, то у него останется 7 рублей, а на покупку 15 тетрадей ему не хватит 5 рублей. Сколько денег у Николая? Ответ обоснуйте.
2. Какова последняя цифра ответа 2003 · 2005 · 2007 – 2000 · 2008? Ответ обоснуйте.
3. Как разложить семь алмазов в четыре одинаковые шкатулки, чтобы вес всех шкатулок получился одинаковым, если вес алмазов 1, 2, 3, 4, 5, 6, 7. граммов. Ответ обоснуйте.
4. На одной чаше весов лежит кусок мыла, на другой 2/3   такого же куска и еще 2/3 кг. Сколько весит весь кусок мыла? Ответ обоснуйте.
5. Четыре ученика – Витя, Петя, Юра и Сергей – заняли на математической Олимпиаде  четыре первых места. На вопрос, какие места они заняли, были даны ответы:

1. Не выполняя деления, выясните, делится ли значение выражения 37 · 124 + 21 · 124 + 58 · 554 на 678. Ответ обоснуйте.
2. Средний возраст 11 игроков футбольной команды 22 года. Когда одного игрока удалили с поля, средний возраст оставшихся игроков составил 21 год. Сколько лет удаленному игроку? Ответ обоснуйте.
3. Какова сумма всех цифр, используемых для записи всех натуральных чисел от 1 до  1 000 000? Ответ обоснуйте.
4. 2% натурального числа А больше, чем 3% натурального числа В. Верно ли, что  5%  числа  А  больше, чем  7%  числа В?  Ответ обоснуйте.
5. Ваня, Петя, Саша и Коля носят фамилии, начинающиеся на буквы В, П, С и К.  Известно, что 

1. Решите уравнение |x - 2007| = 2.
2. Какова сумма всех цифр, используемых для записи всех натуральных чисел от 1 до 1 000 000? Ответ обоснуйте.
3. В школе все учащиеся сидят за партами по двое, причем у 60% мальчиков сосед по парте - тоже мальчик, а у 20% девочек сосед по парте - тоже девочка. Сколько процентов учащихся этой школы составляют девочки?
4. Дана белая доска размером 100 x 100 клеток. Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2 x 2, а второй три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выиграет при правильной игре: первый или второй? Ответ обоснуйте.
5. Найдите сумму внешних углов выпуклого 2007-угольника. Ответ обоснуйте.

1. В параллелограмме АВС биссектриса угла С пересекает сторону А в точке М и прямую АВ  в точке К. Найдите периметр параллелограмма, если АК = 12, СМ = 24, МК = 18.
2. Постройте график функции y = |x - 1| - |2 - x| + 2.
3. Вычислите  .
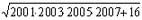4. Решите уравнение x⁴ + 2006x² – 2007 = 0.
5. Токарь и его ученик, работая одновременно, обычно выполняют задание за 4 часа. При этом производительность труда токаря в 2 раза выше производительности ученика. Получив такое же задание, и, работая по очереди, они справились с заданием за 9 часов работы. Какую часть задания выполнил ученик токаря.

1. Вычислите .
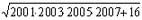2. Решите уравнение 3cosx = x² + 3.
3. Постройте график функции y =|x - 3| + |1 - x| - 4.
4. Докажите, что x⁴ + y ⁴ + z ² + 1 > 2x (xy ² – x + z + 1).
5. Пирамида Хеопса имеет в основании квадрат, а ее боковые грани – равные равнобедренные треугольники. Может ли угол грани при вершине пирамиды быть равным 95 Ответ обоснуйте.

1. Решите уравнение .
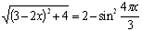2. Функция y = f(x) определена на множестве всех действительных чисел и является периодической с периодом 5. Найдите значение выражения 
     f(-6) + f(19) – f(-13), если f(-1) = -2 и f(2) = 3,5.
3. Какую наибольшую длину может иметь ребро правильного тетраэдра, который помещается в коробку, имеющую форму куба со стороной 1 см? Ответ обоснуйте.
4. Докажите, что x⁴ + y⁴ + z² + 1 >= 2x (xy² – x + z + 1).
5. Сторона основания правильной треугольной пирамиды равняется а, а боковое ребро равняется b. Плоскость, параллельная боковому ребру и проходящая через скрещивающуюся с ним сторону основания, пересекает пирамиду по квадрату. Вычислите сторону квадрата.

Олимпиадные задачи 2 тура с решениями и ответами - 2006 год

6 класс

1. Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого. Найдите уменьшаемое и вычитаемое.
2. Будет ли сумма чисел  1 + 2 + 3 + …..+ 2005 + 2006 + 2007 делиться на 2007? Ответ обоснуйте.
3. Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов. Какое наибольшее число клеток понадобится?
4. На выставку привезли 25 собак. 12 из них большие, 8 – маленькие, остальные средние. Только 10 из участников выставки породистые, остальные – дворняжки. Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?
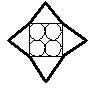
5. Все треугольники, изображенные на рисунке, имеют равные стороны. Радиус каждой из окружностей равен 2 см. Окружности касаются друг друга и сторон квадрата. Чему равен периметр «звездочки», нарисованной жирной линией?

7 класс

1. Восстановите пример: АВС × СВА = 692443.
2. За весну Обломов похудел на 25%, затем за лето поправился на 20%, затем за осень похудел на 10%, а за зиму прибавил 20%. Похудел он в итоге или поправился? Ответ обоснуйте.
3. Какой цифрой оканчивается число 20072006?
4. На клетчатой бумаге со стороной клетки 1 см нарисован треугольник. 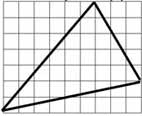Чему равна его площадь?
5. У мамы четыре дочери Поля, Валя, Катя и Маша. Девочки играли и разбили вазу. На вопрос: «Кто это сделал?» Поля, Валя и Катя ответили: «Не я», а Маша – «не знаю». Потом оказалось, что две из них сказали правду, а две неправду. Знает ли Маша, кто разбил вазу? Ответ объясните.

8 класс

1. Решите уравнение x - 6 = |x - 3|/(x - 3).
2. Верно ли равенство 3¹⁰⁰ + 7¹⁰⁰ = 8¹⁰⁰? Ответ обоснуйте.
3. Дворники получают грабли и метлы. Если каждый возьмет одну метлу или одни грабли, то останется 14 метел. А чтобы дать каждому дворнику и одну метлу, и одни грабли, не хватает 10 грабель. Сколько было дворников, сколько метел и сколько грабель?
4. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал туземца узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: «Туземец говорит, что он абориген». Кем был проводник: пришельцем или аборигеном? Ответ обоснуйте.
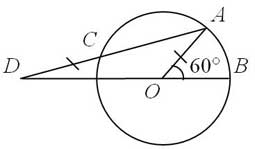
5. В окружности с центром в точке О проведены радиусы ОВ и ОА так, что ﮮАОВ=60°, ОВ = DС. Найдите величину ﮮАDО.

9 класс

1. В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.
2. Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
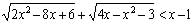
3. Решите неравенство .
4. Решите уравнение x² + 2005x – 2006 = 0.
5. Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?

10 класс 

1. Решите уравнение (x-2)(x-3)(x+4)(x+5) = 1320.
2. На плоскости дан отрезок АВ. Где может быть расположена точка С, чтобы ∆АВС был остроугольным?
3. Найти все натуральные числа, оканчивающиеся на 2006, которые после зачеркивания последних   четырех цифр уменьшаются в целое число раз.
4. Вычислить сумму a²⁰⁰⁶ + 1/a²⁰⁰⁶, если a²– a + 1 = 0.
5. Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей, и т. д. Может ли за некоторое число разрезаний получиться 2006 листка бумаги?

11 класс

1. Докажите, что уравнение  xy = 2006 (x+y) имеет решения в целых числах.
2. Докажите, что если α, β, γ - углы произвольного треугольника, то справедливо тождество cos²α + cos²β + cos²γ + 2 cosα cosβ cosγ = 1.
3. Три шара радиуса R касаются друг друга и плоскости  α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных  шаров. Определите высоту «горки» из четырех шаров.
4. Докажите неравенство x² - 3x³ < 1/6 на луче [1/4; +∞).
5. В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.