Учимся вместе

Олимпиадные задачи 2 тура с решениями и ответами - 2009 год

 7 класс

1. В данном примере различные цифры зашифрованы различными буквами. Определите, какое равенство зашифровано: ОТВЕТ + ОЧЕНЬ = ПРОСТ.
2. В спортивной секции девочки составляют 60% числа мальчиков. Сколько процентов числа всех участников секции составляют девочки?
3. Найти наименьшее шестизначное число, делящееся на 9, все цифры которого различны.
4. Можно ли квадрат со стороной 1 м разрезать на 7 прямоугольников, не обязательно одинаковых, каждый из которых имел бы периметр 2 м?
5. Можно ли покрасить клетчатый квадрат 2009 x 2009 в два цвета – черный и белый (каждая единичная клетка красится одним из этих цветов) – таким образом, чтобы каждая черная клетка имела двух белых соседей, а каждая белая клетка – двух черных соседей (соседями считаем клеточки, которые имеют общую сторону)? Ответ обоснуйте.
   

8 класс

1. Докажите, что 13 + 13² + 13³ + 13⁴ +…+ 13²⁰⁰⁹ + 13²⁰¹⁰ делится нацело на 7.
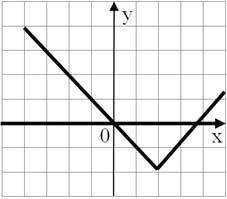
2. Постройте график функции y = |x - 2| - 2.
3. На сторонах АВ, ВС и АС равностороннего треугольника АВСвзяты соответственно точки D, E, F, так что AD = BE = CF. Каков вид треугольника DEF? Докажите.
4. Известно, что a + b + c = 5, ab + ac + bc = 5. Чему может равняться a² + b² + c²?
5. На 44 деревьях, расположенных по кругу, сидели по веселому чижу. Время от времени какие-то два чижа перелетают на соседнее дерево – один по часовой стрелке, а другой – против. Могут ли все чижи собраться на одном дереве?
   

9 класс

1. На доске написаны восемь простых чисел, каждое из которых больше двух. Может ли их сумма равняться 59?
2. В хоре число девочек относилось к числу мальчиков как 4:3. После того как в хор пришли двое новеньких, это соотношение стало 3:2. Сколько мальчиков было в хоре вначале?
3. В четырехугольнике ABCD диагонали пересекаются в точке M. Известно, что AM = 1, BM = 2, CM = 4. При каких значениях DM четырехугольник ABCD является трапецией?
4. Сравните числа √2011 + √2009 и 2√2010.
5. Докажите, что среди любых шести человек найдутся трое знакомых или трое незнакомых между собой людей.

10 класс

1. Пусть a + b + c < 0 и уравнение ax² + bx + c = 0 не имеет корней. Какой знак имеет число c?
2. Докажите, что уравнение xy = 2009 (x + y) имеет решения в целых числах.
3. Окружность, построенная на катете прямоугольного треугольника, как на диаметре, делит гипотенузу в отношении 1:3. Определить углы треугольника.
4. (an) – арифметическая прогрессия с разностью 1. Известно, что S2009 - наименьшая среди всех S_n (меньше суммы первых n членов для любого другого значения n). Какие значения может принимать первый член прогрессии?
   Имеется три кучи камней: в первой – 10, во второй – 15, в третьей – 20 камней. За ход разрешается разбить любую кучу на две меньшие. Проигрывает тот, кто не сможет сделать ход. Кто победит – начинающий или его партнер?

11 класс

1. Постройте график функции 
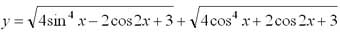
2. Определите a так, чтобы сумма квадратов корней уравнения x² + (2 - a)x – a - 3 = 0 была наименьшей.
3. Докажите, что если число 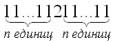 делится на 11, то оно также делится и на 121. 
4. Длины четырех отрезков (числа a, b, c, d) удовлетворяют условию a² + b² + c² + d² = ab + bc + cd + da. Верно ли, что объем куба, ребро которого равно одному из этих отрезков, равен объему прямоугольного параллелепипеда, тремя ребрами которого являются три другие отрезка?
5. Даны n точек, никакие четыре из которых не принадлежат одной плоскости. Сколько плоскостей можно провести через различные тройки этих точек?

Ответы и решения задач

2009 год

7 класс

1. Зашифрованное равенство:  34214 + 35170 = 69384.
    
2. Ответ: 37,5%. Пусть в спортивной секции было х мальчиков, тогда девочек – 0,6х. Они составляют (0,6x 100)/(x + 0,6x).
    
3. Ответ: 102348. Наименьшее число должно начинаться так: 10234. Последнюю цифру подбираем таким образом, чтобы выполнялся признак делимости на 9.
    
4. Ответ: можно. Например, отрезав по периметру квадрата 4 прямоугольника со сторонами 7/8 м и 1/8 м, а потом разрезать квадрат, который остался, на 3 прямоугольника со сторонами 3/4 м и 1/4 м.
    
5. Ответ: нельзя. Предположим, что такое заполнение возможно, и подсчитаем количество единичных отрезков, служащих общей границей соседних черной и белой клеток. С одной стороны, каждый такой отрезок примыкает ровно к одной белой клетке, и по условию к каждой белой клетке примыкает ровно два таких отрезка. Следовательно, количество рассматриваемых отрезков равняется удвоенному количеству белых клеток. Аналогично количество рассматриваемых отрезков равняется удвоенному количеству черных клеток. Но тогда, белых и черных клеток должно быть поровну, что невозможно. Так как их общее количество 20092 - нечетное число.

8 класс

1. Доказательство: 13 + 13² + 13³ + 13⁴ + … + 13²⁰⁰⁹ + 13²⁰¹⁰ = 13 (1 + 13) + 13³(1 + 13) + … + 13²⁰⁰⁹(1 + 13) = 14 (13 + 13³ + … + 13²⁰⁰⁹). Так как 14 делится на 7, то и само число делится нацело на 7.


2. 
3. 
   
   
   Ответ: равносторонний. Т.к. ∆ DBE = ∆ ECF = ∆ FAD (по двум сторонам и углу между ними). То DE = EF = FD. Поэтому ∆ DEF – равносторонний.
   
   
   
4.  
5. 
   
   
   Ответ: 15. Пронумеруем деревья по кругу с 1-го по 44-е. Сумма номеров деревьев, на которых сидят чижи либо не меняется, либо уменьшается на 44, либо увеличивается на 44. Тем самым, остаток от деления этой суммы номеров на 44 не меняется. Изначально этот остаток равен 22, а если все чижи усядутся на одно дерево, то он будет равен нулю. Поэтому чижи не смогут собраться на одном дереве.

9 класс

1. Ответ: Нет. Сумма не может получиться нечетной, так как все простые числа, кроме двойки, - нечетные, а сумма восьми нечетных чисел четна.
2. Ответ: Мальчиков было 12. Решение: пусть вначале было 4x девочек, 3x мальчиков. Пусть среди новеньких a девочек. Тогда (4x + a) : (3x + (2 – a)) = 3:2. Отсюда x = 5a - 6 Единственно возможное значение a = 2 приводит к x = 4.
3. Ответ: Четырехугольник ABCD является трапецией, если DM равно 8 или 0,5. Возможны два варианта: основаниями трапеции являются стороны AB и CD или AD и BC. Рассмотрим первый случай: ∆ АМВ должен быть подобен ∆ СМD, откуда AM : MC = BM : DM, DM = 8. Во втором случае подобными треугольниками будут AMD и BMC. Тогда AM : MC = BM : DM, откуда DM = 0,5.
4. Пусть 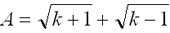, B = 2√k , где k= 2010. Тогда  A² – B² =  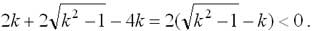Поэтому A <B.
5. Пусть эти шестеро: A, B, C, D, E, M. А находится в одном из двух отношений «знаком» или «незнаком» хотя бы с тремя из них. Пусть это будут Если какие-то два из них находятся в том же отношении друг с другом, то они вместе с А образуют искомую тройку. В противном случае искомая тройка B, C, D.

10 класс

1. Ответ: c < 0. Обозначим за  f(x) = ax² + bx + c.  Т.к.  f(1) = a + b + c< 0, то график функции f(x) = ax² + bx + c будет находиться ниже оси абсцисс,
   а значит,   f(0) = c< 0.
2. Преобразуем уравнение к следующему виду:  (x - 2009)(y - 2009) = 2009². Уравнение имеет решения, например, x = y = 4018.
3. Ответ: ﮮA = 30°, ﮮВ = 60° илиﮮA = 60°, ﮮВ = 30°. Необходимо рассмотреть два случая.
4. Ответ: a €(-2009; -2008). Так как разность прогрессии положительна, то прогрессия – возрастающая. Следовательно, описанная ситуация возможна тогда и только тогда, когда члены прогрессии с первого по 2009-ый – отрицательны, а начиная с 2010-го – положительны. Таким образом, S₂₀₀₉ будет наименьшей, тогда и только тогда, когда а₂₀₀₉ <0, a₂₀₁₀ > 0. Отсюда получаем систему неравенств
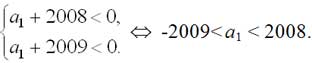
5. После каждого хода количество кучек увеличивается на 1. Сначала их было 3, в конце – 45. Всего будет сделано 42 хода, последний ход сделает второй игрок и выиграет.

11 класс

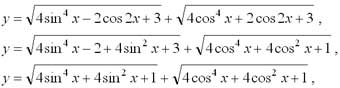1. y = 4. Поэтому, графиком функции будет прямая, заданная уравнением y = 4.
2. Ответ:  a = 1.   Найдем сумму квадратов корней уравнения  x₁² +  x₂²  = (x₁ +  x₂)² – 2x₁x₂ = (2 – a)² + 2(a + 3) = … = (a – 1)² + 9. Значение данного выражения будет наименьшим при  a = 1. При этом значении a дискриминант левой части уравнения положителен, поэтому корни существуют.
3. Имеем 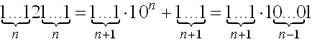. Из условия следует, что хотя бы один сомножитель делится на 11. Если первый, то n + 1 четно, если второй, то n  - 1 четно, в силу признака делимости на 11. Тогда оба числа n + 1 и n  - 1 четны, оба сомножителя делятся на 11, и их произведе­ние делится на 121.
4. Ответ: да, верно. Данное уравнение перепишем в виде  (a – b)² + (b – c)² + (c– d)² + (d – a)² = 0. Следовательно, длины всех четырех отрезков равны между собой. Поэтому объем куба с ребром a равен объему прямоугольного параллелепипеда с ребрами b,  c, d.
5. Ответ: (n(n - 1)(n - 2))/6 . Первую точку можно взять п способами, вторую
   (n – 1)  способом. Число прямых, проходящих через них, равно (n(n - 1)/2. Третью точку можно выбрать (n – 2) способами. Тогда число прямых, проходящих через эти три точки, равно (n(n - 1)(n - 2))6, что и определяет наибольшее количество плоскостей, которые можно провести через различные тройки из n точек.