Учимся вместе

 Олимпиадные задачи 2 тура с решениями и ответами - 2008 год

2008 год

7 класс

1. Найдите все корни уравнения |х - 2008| = 2009.
2. Гонцу надо было пробежать 24 мили. Две трети этого расстояния он бежал со средней скоростью 8 миль в час. Сможет ли он, увеличив скорость, пробежать остаток пути так, чтобы его средняя скорость на всем пути оказалась равной 12 миль в час.
3. Дима взял 2008 одинаковых квадратиков. Он хочет сложить из всех этих квадратиков прямоугольник. Сколько различных прямоугольников он может получить?
4. Четверо купцов заметили, что если они сложатся без первого, то соберут 90 рублей, без второго – 85, без третьего – 80, без четвертого – 75 рублей. Сколько у кого денег?
5. Последовательность чисел строится по следующему закону. На первом месте стоит число 7, далее за каждым числом стоит сумма цифр его квадрата, увеличенная на единицу. Например, на втором месте стоит число 14, так как  7² = 49, а 4 + 9 + 1 = 14.  На третьем месте стоит число 17 и так далее. Какое число стоит на 2008-м месте?

8 класс

1. Корень из числа 49 можно извлечь по такой «формуле»: √ 49 = 4 + √9.
2. Существуют ли другие двузначные числа, квадратные корни из которых извлекаются аналогичным образом и являются целыми? Укажите все такие двузначные числа.
3. ABC – равнобедренный треугольник с вершиной А. ﮮА=27°. Точка D симметрична точке В относительно А. Чему равен угол ﮮBCD?
4. Мальчик стоит на автобусной остановке и мёрзнет, а автобуса нет. Ему хочется пройтись до следующей остановки. Мальчик бегает вчетверо медленнее автобуса и может увидеть автобус на расстоянии 2 км. До следующей остановки ровно километр. Имеет ли смысл идти, или есть риск упустить автобус?
5. Про числа aи b известно, что a = b+ 1. Может ли оказаться так, что
   a⁴  =  b⁴?
6. Какое наименьшее количество клеток квадрата 5 x 5 нужно закрасить, чтобы в любом квадрате 3 x 3, являющемся его частью, было ровно
   4 закрашенных клетки?

9 класс

1. Докажите, что число  2008² + 2008² ×  2009² + 2009²  является ли квадратом целого числа.
2. Рассматриваются функции вида y = x² + ax + b, где  а + b = 2008. Докажите, что графики всех таких функций имеют общую точку.
3. На острове рыцарей и лжецов (лжецы всегда лгут, рыцари всегда говорят правду) каждый болеет ровно за одну футбольную команду. В опросе приняли участие все жители острова. На вопрос «Болеете ли Вы за «Спартак»?» ответили «Да» 40% жителей. На аналогичный вопрос про «Зенит» утвердительно ответили 30%, про «Локомотив» - 50%, а про ЦСКА – 0%. Какой процент жителей острова действительно болеет за «Спартак»?
4. В выпуклом пятиугольнике ABCDE  ﮮА = ﮮB =ﮮD = 90°. Найдите ﮮADB, если известно, что в данный пятиугольник можно вписать окружность.
5. Кольцевая дорога поделена столбами на километровые участки, и известно, что количество столбов четно. Один из столбов покрашен в желтый цвет, другой - в синий, а остальные – в белый. Назовем расстояние между столбами длину кратчайшей из двух соединяющих их дуг. Найдите расстояние от синего столба до желтого, если сумма расстояний от синего столба до белых равна 2008 км. 

10 класс

1. Графики функций  у = х² + ах + bи  у = х² + сх + d  пересекаются в точке с координатами  (1; 1).  Сравните  a⁵ + d⁶ и  c⁶- b⁵.
2. Какое наибольшее число ребер шестиугольной призмы может пересечь плоскость, не проходящая через вершины призмы?
3. Решите уравнение : 
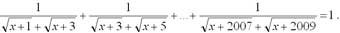4. Докажите, что если стороны треугольника образуют геометрическую прогрессию, то их высоты тоже образуют геометрическую прогрессию.
5. В клетки квадрата 3 × 3 требуется вписать девять различных натуральных чисел так, чтобы все они не превосходили n, и чтобы произведения чисел в каждой строке и каждом столбце были равны. При каком наименьшем n это возможно?

11 класс

1. Найдите такое натуральное число k, что 2008! делится на 2007^k, но не делится на 2008^k. (Напомним, чтоn! = 1·2·3·4·… ·n).
2. Может ли вершина параболы y = 4x² – 4(a + 1)x + a  лежать во второй координатной четверти при каком-нибудь значении а?
3. (a_n) – арифметическая прогрессия с разностью 1. Известно, что S₂₀₀₈ - наименьшая среди всех S_n (меньше суммы первых n членов для любого другого значения n). Какие значения может принимать первый член прогрессии?
4. Внутри равностороннего треугольника со стороной 8 находится равнобедренный треугольник АВС, в котором АС = ВС = 1, ﮮС=120°. Две вершины А и В могут лежать либо на одной стороне большого треугольника, либо на двух. Где при этом может оказаться вершина тупого угла – точка С? Нарисуйте это геометрическое место точек и найдите длину соответствующей линии.
5. Клетчатая прямоугольная сетка m x n связана из веревочек единичной длины. Двое делают ходы по очереди. За один ход можно разрезать (посередине) не разрезанную ранее единичную веревочку. Если не останется ни одного замкнутого веревочного контура, то игрок, сделавший последний ход, считается проигравшим. Кто из игроков победит при правильной игре и как он должен для этого играть?

Ответы и решения задач

2008 год

7 класс

1. Ответ:  4017  и  -1.
2. Нет, не может. Для того, чтобы средняя скорость гонца, пробежавшего 24 мили, была равна 12 милям в час, необходимо, чтобы он пробежал этот путь за 2 часа. Но из условия следует, что за два часа гонец пробежал только 16 миль.
3. Ответ: 4.
4. Всего денег у купцов (90 + 85 + 80 + 75) : 3 = 110 рублей. Поэтому у первого 110 – 90 = 20, у второго 110 – 85 = 25, у третьего 110 – 80 = 30, а четвертого 110 – 75 = 35 рублей.
5. Вычислим несколько первых членов данной последовательности: 7; 14; 17; 20; 5; 8;11;5; 8; 11; 5; … Таким образом, начиная с пятого члена последовательности, будет повторяться одна и та же тройка чисел 5, 8, 11. Так как 2008 – 4 = 2004, а 2004 кратно 3, то на 2008-м месте будет стоять число 11.

8 класс

1. Да, существуют: 64 и 81. Рассмотрим все двузначные числа, являющиеся квадратами целых чисел. Корни из чисел 16, 25 и 36 не могут быть извлечены указанным способом, так как квадратные корни из их последних цифр не являются целыми. Числа 49, 64 и 81 являются решениями. Ответ в задаче не изменится, если не требовать, чтобы корень был целым. Действительно, если , то 10a + b = a² + 2a√b + b. Так как в левой части равенства стоит целое число, то и число, стоящее в правой части, должно быть целым. Отсюда следует, что b = 0, 1, 4 или 9, то есть a + √b  - целое число.
2. Ответ: 90°.
3. Ответ: имеет смысл идти. Пусть мальчик пошел к следующей остановке и в какой-то момент заметил автобус. Скорость автобуса в четыре раза больше скорости мальчика, поэтому за одно и то же время автобус проезжает расстояние в четыре раза больше. Пусть мальчик пробежит х км, тогда автобус проедет 4х км. В случае, если они двигаются навстречу друг другу, до встречи с автобусом мальчик пробежит 2/5 км. Это значит, что, отойдя от остановки не более, чем на 2/5 км, мальчик сможет успеть на автобус, побежав назад. В случае, если автобус догоняет мальчика, мальчик успеет пробежать 2/3 км до момента, когда автобус его догонит. Это означает, что он сможет успеть на автобус, если до следующей остановки осталось не более 2/3  км, то есть, если он успел пройти не менее  1/3 км до момента, когда заметил автобус. Так как,  1/3 <  2/5 , то у мальчика всегда будет возможность успеть на автобус и имеет смысл идти.
4. Ответ: да, может. Пусть а = 1/2, b = -1/2, тогда a⁴ = b⁴ = 1/16. Можно доказать, что этот пример – единственный (от учащихся это не требуется). Действительно, a⁴ = b⁴ ⇔ |a| = |b|. Случай a = b невозможен, случай a = -b дает указанный пример.
5. Ответ: 7 клеток. Покажем, что придётся закрасить не менее семи клеток. 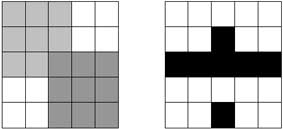Рассмотрим два квадрата 3 > 3 (см. рисунок слева). В каждом их этих квадратов должно быть закрашено по четыре клетки. Так как их общая часть составляет одну клетку, то в них не может быть закрашено менее семи клеток. Один из возможных примеров с семью закрашенными клетками приведён на рисунке справа.

9 класс

1. Рассмотрим выражение n² + n² (n + 1)²  + (n + 1)² = n⁴+ 2n³ + 2n² + (n + 1)² = n⁴+ 2n² (n + 1) + (n + 1)² = (n² + n + 1)². Данное число есть значение этого выражения при n = 2008. Значит, 2008² + 2008²∙2009² + 2009² = (2008² + 2009)² – квадрат целого числа.
2. y(1) = 1 + a + b = 2009. Следовательно, каждый из данных графиков проходит через точку с координатами (1; 2009).
3. Пусть x% жителей острова составляют лжецы. Тогда (100 – х)% составляют рыцари. Так как каждый рыцарь утвердительно ответил ровно на один из вопросов, а каждый лжец – на три, то (100 – х) + 3х = 40 + 30 + 50, откуда х = 10. Так как ни один из жителей острова не сказал, что болеет за ЦСКА, то все лжецы болеют за ЦСКА. Каждый из них заявил, что болеет за «Спартак», поэтому действительно болеют за «Спартак» 40% - 10% = 30% жителей.
4. Пусть О - центр окружности, вписанной в пятиугольник АВСDE. Проведем перпендикуляры ОК, ОL, OM, ON и OT_K сторонам AB, BC, CD, DEи EAсоответственно. Поскольку проведенные отрезки являются радиусами окружности, то четырехугольники AKOT, KBLO иOMDN - равные квадраты. Диагонали  OA, OBи ODрассмотренных квадратов равны, поэтому О – центр окружности, описанной около ∆ ADB. Следовательно, ﮮADB = 1/2ﮮAOB = 45°. (Учащиеся могут предложить и другие способы нахождения угла ADB,например, используя свойства отрезков касательных и формулу для нахождения суммы внутренних углов выпуклого пятиугольника).
5. Пусть на кольцевой дороге – 2n столбов. Вычислим сумму расстояний от синего столба до всех остальных: 2(1 + 2 + …+ (n– 1)) + n = 2((1 + n -1)/2) n + n = n² (км). Следовательно, n² > 2008. Учитывая, что n – натуральное число, получим, что n ≥ 45. Так как расстояние от синего столба до желтого не превосходит n, то n² – n ≤ 2008 n(n – 1) ≤ 2008. Несложно проверить, что n = 45 удовлетворяет этому неравенству, а любое натуральное n, начиная с 46, - не удовлетворяет. Тогда n² = 2025, следовательно, расстояние от синего столба до желтого равно 2025 – 2008 = 17.
   Ответ: 17 км.

10 класс

1. Ответ: a⁵ + d⁶ = c⁶ – b⁵.
   Так как графики функций проходят через точку (1; 1), то выполняются равенства: 1 = 1 + а + b и 1 = 1 + с + d, то есть, a = -b и с = -d. Следовательно, а⁵ = -b⁵ и d⁶ = c⁶. Складывая эти неравенства почленно, получим, что а⁵ + d⁶ = c⁶ – b⁵.
2. Ответ: 8.
   Горизонтальной плоскостью можно пересечь все 6 боковых ребер. Наклоним эту плоскость так, чтобы она пересекла верхнее основание около одной из вершин. Ясно, что при этом она станет пересекать два ребра в верхнем основании, но перестанет пересекать одно из боковых ребер. Таким образом, мы увеличим число пересеченных ребер на 1.
   Точно также можно увеличить это число еще на 1 за счет ребер нижнего основания. Так мы получили плоскость, пересекающую 8 ребер призмы.
   Почему больше пересечений получить невозможно? Во-первых, никакое сечение не может пересекать более двух ребер одного основания (иначе сечение просто совпадает с плоскостью этого основания). Но пересечение двух ребер в одном основании исключает пересечение хотя бы одного из боковых ребер, а пересечение двух ребер в другом основании – другого бокового ребра.
3. Ответ:  251000.  Умножим числитель и знаменатель каждой дроби на выражение, сопряженное знаменателю: 
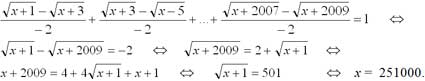
4. Пусть стороны треугольника равны b, bq, bq², площадь треугольника S, тогда высоты треугольника соответственно равны: 2S/b, 2S/bq, 2S/db², то есть тоже образуют геометрическую прогрессию.
5. Покажем, что n = 14 слишком мало. Среди чисел 1, 2, …, 14 только 2 делятся на 5 (5 и 10), поэтому их нельзя использовать (не во всех строках произведение будет делиться на 5). По тем же соображениям нельзя использовать числа 7 и 14. Тем более, нельзя использовать числа 11 и 13. Итак, 6 чисел уже отпадают. Остается всего 8 чисел, а их не хватит для заполнения клеток квадрата! На рисунке изображен квадрат с n = 15.
    

11 класс 

1. Ответ: 9. Разложим число 2007 на простые множители: 2007 = 3² ∙ 223.
   В разложении на простые множители числа 2007! показатель степени у числа 3 будет достаточно большим, так как множитель 3 входит в разложение каждого третьего числа. Множитель 223 входит только в разложение чисел вида 223р, где р – натуральное число, не превосходящее 9. Таким образом, в разложение числа 2007! на простые множители число 223 войдет с показателем 9. Следовательно, число 2008! будет делиться на 2007^k, где k=9.
2. Ответ: нет, не может.   Координаты вершины параболы x = (a + 1)/2, y = 4((a + 1)/2)² - 4(a +1)(a + 1)/2 + a = -a² - a - 1 = -(a + 1/2)² - 3/4. Так как у < 0 при любых значениях а, то во второй координатной четверти вершина параболы находиться не может.
3. Ответ: a₁ (-2008; -2007). Так как разность прогрессия положительна, то прогрессия – возрастающая. Следовательно, описанная ситуация возможна тогда и только тогда, когда члены прогрессия с первого по 2008-ой – отрицательны, а начиная с 2009-го – положительны. Таким образом, S2008 будет наименьшей, тогда и только тогда, когда а₂₀₀₈ < 0, a₂₀₀₉ > 0. Отсюда получаем систему неравенств
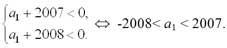
4. Если вершина А и В лежат на одной стороне треугольника, то вершина С лежит на отрезке прямой, параллельной этой стороне. Длина этого отрезка равна 8 - √3. Пусть вершины А и В лежат на двух сторонах равностороннего треугольника с общей вершиной О. Тогда вокруг четырехугольника АСВО можно описать окружность (четырехугольник является вписан­ным). В этой окружности углы ВАС и ВОС равны, так как опираются на одну и ту же дугу с хордой ВС. Следовательно, угол ВОС равен 30°. 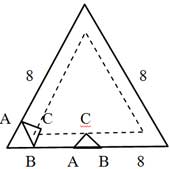Следовательно, третья вершина треугольника – точка С – лежит на биссектрисе угла равностороннего треугольника. Длина соответствующего отрезка биссектрисы равна 1. Итак, точка С может лежать на стороне некоторого равностороннего треугольника и на некоторых отрезках биссектрис внутренних углов этого треугольника. Длина шести звеньев этой ли­нии равна 27 - 3√3.
5. Ответ: если m + n – четно, то выигрывает второй игрок, если m + n – нечетно, то выигрывает первый. В начале игры веревочек единичной длины было m(n + 1) + n(m + 1) = 2mn + m + n. Это число имеет ту же четность, что и число m + n. Последний ход в игре разрушает последний замкнутый контур. Докажем, что граница любого замкнутого конура содержит четное количество веревочек единичной длины. Действительно, рассмотрим границу произвольного замкнутого контура. Каждый вертикальный столбец исходной сетки содержит четное количество горизонтальных веревочек единичной длины из этой границы (возможно, и нулевое), т. к. войдя в замкнутый контур, на­пример, снизу, мы обязаны из него выйти. Аналогично, каждая горизонтальная строка исходной сетки содержит четное количество вертикальных веревочек единичной длины. Таким образом, общее количество единич­ных веревочек на границе замкнутого контура – четно. Выигрышная стратегия для любого игрока состоит в том, чтобы не разрушать последний замкнутый контур, пока есть такая возможность.