Учимся вместе

Олимпиадные задачи 2 тура с решениями и ответами - 2007 год

1. Если Коля купит 11 тетрадей, то у него останется 7 рублей, а на покупку 15 тетрадей ему не хватит 5 рублей. Сколько денег у Николая? Ответ обоснуйте.
2. Какова последняя цифра ответа 2003 · 2005 · 2007 – 2000 · 2008? Ответ обоснуйте.
3. Как разложить семь алмазов в четыре одинаковые шкатулки, чтобы вес всех шкатулок получился одинаковым, если вес алмазов 1, 2, 3, 4, 5, 6, 7. граммов. Ответ обоснуйте.
4. На одной чаше весов лежит кусок мыла, на другой 2/3   такого же куска и еще 2/3 кг. Сколько весит весь кусок мыла? Ответ обоснуйте.
5. Четыре ученика – Витя, Петя, Юра и Сергей – заняли на математической Олимпиаде  четыре первых места. На вопрос, какие места они заняли, были даны ответы:

1. Не выполняя деления, выясните, делится ли значение выражения 37 · 124 + 21 · 124 + 58 · 554 на 678. Ответ обоснуйте.
2. Средний возраст 11 игроков футбольной команды 22 года. Когда одного игрока удалили с поля, средний возраст оставшихся игроков составил 21 год. Сколько лет удаленному игроку? Ответ обоснуйте.
3. Какова сумма всех цифр, используемых для записи всех натуральных чисел от 1 до  1 000 000? Ответ обоснуйте.
4. 2% натурального числа А больше, чем 3% натурального числа В. Верно ли, что  5%  числа  А  больше, чем  7%  числа В?  Ответ обоснуйте.
5. Ваня, Петя, Саша и Коля носят фамилии, начинающиеся на буквы В, П, С и К.  Известно, что 

1. Решите уравнение |x - 2007| = 2.
2. Какова сумма всех цифр, используемых для записи всех натуральных чисел от 1 до 1 000 000? Ответ обоснуйте.
3. В школе все учащиеся сидят за партами по двое, причем у 60% мальчиков сосед по парте - тоже мальчик, а у 20% девочек сосед по парте - тоже девочка. Сколько процентов учащихся этой школы составляют девочки?
4. Дана белая доска размером 100 x 100 клеток. Двое по очереди красят ее клетки в черный цвет, причем первый всегда закрашивает квадрат 2 x 2, а второй три клетки, образующие «уголок». Уже покрашенную клетку второй раз красить нельзя. Проигрывает тот, кто не может сделать очередной ход. Кто выиграет при правильной игре: первый или второй? Ответ обоснуйте.
5. Найдите сумму внешних углов выпуклого 2007-угольника. Ответ обоснуйте.

1. В параллелограмме АВС биссектриса угла С пересекает сторону А в точке М и прямую АВ  в точке К. Найдите периметр параллелограмма, если АК = 12, СМ = 24, МК = 18.
2. Постройте график функции y = |x - 1| - |2 - x| + 2.
3. Вычислите  .
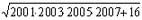4. Решите уравнение x⁴ + 2006x² – 2007 = 0.
5. Токарь и его ученик, работая одновременно, обычно выполняют задание за 4 часа. При этом производительность труда токаря в 2 раза выше производительности ученика. Получив такое же задание, и, работая по очереди, они справились с заданием за 9 часов работы. Какую часть задания выполнил ученик токаря.

1. Вычислите .
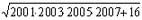2. Решите уравнение 3cosx = x² + 3.
3. Постройте график функции y =|x - 3| + |1 - x| - 4.
4. Докажите, что x⁴ + y ⁴ + z ² + 1 > 2x (xy ² – x + z + 1).
5. Пирамида Хеопса имеет в основании квадрат, а ее боковые грани – равные равнобедренные треугольники. Может ли угол грани при вершине пирамиды быть равным 95 Ответ обоснуйте.

1. Решите уравнение .
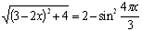2. Функция y = f(x) определена на множестве всех действительных чисел и является периодической с периодом 5. Найдите значение выражения 
     f(-6) + f(19) – f(-13), если f(-1) = -2 и f(2) = 3,5.
3. Какую наибольшую длину может иметь ребро правильного тетраэдра, который помещается в коробку, имеющую форму куба со стороной 1 см? Ответ обоснуйте.
4. Докажите, что x⁴ + y⁴ + z² + 1 >= 2x (xy² – x + z + 1).
5. Сторона основания правильной треугольной пирамиды равняется а, а боковое ребро равняется b. Плоскость, параллельная боковому ребру и проходящая через скрещивающуюся с ним сторону основания, пересекает пирамиду по квадрату. Вычислите сторону квадрата.

Олимпиадные задачи 2 тура с решениями и ответами - 2006 год

6 класс

1. Разность двух чисел на 17 меньше уменьшаемого и на 9 больше вычитаемого. Найдите уменьшаемое и вычитаемое.
2. Будет ли сумма чисел  1 + 2 + 3 + …..+ 2005 + 2006 + 2007 делиться на 2007? Ответ обоснуйте.
3. Нужно разместить 17 кроликов так, чтобы в каждой клетке было разное количество кроликов. Какое наибольшее число клеток понадобится?
4. На выставку привезли 25 собак. 12 из них большие, 8 – маленькие, остальные средние. Только 10 из участников выставки породистые, остальные – дворняжки. Среди дворняжек поровну больших, маленьких и средних. Сколько больших породистых собак привезли на выставку?
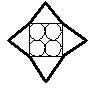
5. Все треугольники, изображенные на рисунке, имеют равные стороны. Радиус каждой из окружностей равен 2 см. Окружности касаются друг друга и сторон квадрата. Чему равен периметр «звездочки», нарисованной жирной линией?

7 класс

1. Восстановите пример: АВС × СВА = 692443.
2. За весну Обломов похудел на 25%, затем за лето поправился на 20%, затем за осень похудел на 10%, а за зиму прибавил 20%. Похудел он в итоге или поправился? Ответ обоснуйте.
3. Какой цифрой оканчивается число 20072006?
4. На клетчатой бумаге со стороной клетки 1 см нарисован треугольник. 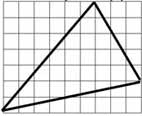Чему равна его площадь?
5. У мамы четыре дочери Поля, Валя, Катя и Маша. Девочки играли и разбили вазу. На вопрос: «Кто это сделал?» Поля, Валя и Катя ответили: «Не я», а Маша – «не знаю». Потом оказалось, что две из них сказали правду, а две неправду. Знает ли Маша, кто разбил вазу? Ответ объясните.

8 класс

1. Решите уравнение x - 6 = |x - 3|/(x - 3).
2. Верно ли равенство 3¹⁰⁰ + 7¹⁰⁰ = 8¹⁰⁰? Ответ обоснуйте.
3. Дворники получают грабли и метлы. Если каждый возьмет одну метлу или одни грабли, то останется 14 метел. А чтобы дать каждому дворнику и одну метлу, и одни грабли, не хватает 10 грабель. Сколько было дворников, сколько метел и сколько грабель?
4. На острове живут два племени: аборигены и пришельцы. Аборигены всегда говорят правду, а пришельцы всегда лгут. Путешественник, приехавший на остров, нанял островитянина в проводники. Они пошли и увидели другого островитянина. Путешественник послал туземца узнать, к какому племени принадлежит этот туземец. Проводник вернулся и сказал: «Туземец говорит, что он абориген». Кем был проводник: пришельцем или аборигеном? Ответ обоснуйте.
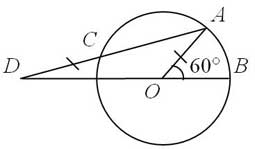
5. В окружности с центром в точке О проведены радиусы ОВ и ОА так, что ﮮАОВ=60°, ОВ = DС. Найдите величину ﮮАDО.

9 класс

1. В трапеции длина одной из диагоналей равна сумме длин оснований, а угол между диагоналями равен 60°. Докажите, что трапеция – равнобедренная.
2. Имеются два сосуда, в первом из них 1 л воды, второй сосуд пустой. Последовательно проводятся переливания из первого сосуда во второй, из второго в первый и т. д., причем доля отливаемой воды составляет последовательно 1/2, 1/3, 1/4 и т. д. от количества воды в сосуде, из которого вода отливается. Сколько воды будет в сосудах после 2007 переливаний?
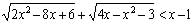
3. Решите неравенство .
4. Решите уравнение x² + 2005x – 2006 = 0.
5. Стрелок десять раз выстрелил по стандартной мишени и выбил 90 очков. Сколько попаданий было в семерку, восьмерку и девятку, если десяток было четыре, а других попаданий и промахов не было?

10 класс 

1. Решите уравнение (x-2)(x-3)(x+4)(x+5) = 1320.
2. На плоскости дан отрезок АВ. Где может быть расположена точка С, чтобы ∆АВС был остроугольным?
3. Найти все натуральные числа, оканчивающиеся на 2006, которые после зачеркивания последних   четырех цифр уменьшаются в целое число раз.
4. Вычислить сумму a²⁰⁰⁶ + 1/a²⁰⁰⁶, если a²– a + 1 = 0.
5. Лист бумаги разрезали на 5 частей, некоторые из этих частей разрезали на 5 частей, и т. д. Может ли за некоторое число разрезаний получиться 2006 листка бумаги?

11 класс

1. Докажите, что уравнение  xy = 2006 (x+y) имеет решения в целых числах.
2. Докажите, что если α, β, γ - углы произвольного треугольника, то справедливо тождество cos²α + cos²β + cos²γ + 2 cosα cosβ cosγ = 1.
3. Три шара радиуса R касаются друг друга и плоскости  α, четвертый шар радиуса R положен сверху так, что касается каждого из трех данных  шаров. Определите высоту «горки» из четырех шаров.
4. Докажите неравенство x² - 3x³ < 1/6 на луче [1/4; +∞).
5. В прямоугольник 20 x 25 бросают 120 квадратов 1 x 1. Докажите, что в прямоугольник можно поместить круг с диаметром, равным 1, не имеющий общих точек ни с одним из квадратов.

Олимпиадные задачи 2 тура предметных Олимпиад школьников по математике

2005 год

9 класс

1. Все трехзначные числа записаны в ряд: 100  101  102 … 998  999. Сколько раз в этом ряду после двойки идет нуль?
2. По определению, n ! = 1 · 2 · 3 · … · n . Какой сомножитель нужно вычеркнуть из произведения 1! · 2! · 3! · … · 20!, чтобы оставшееся произведение стало квадратом некоторого натурального числа?
3. С помощью циркуля и линейки разделите пополам угол, вершина которого недоступна.
4. Сколько существует треугольников со сторонами 5 см и 6 см, один из углов которого равен 20°?На столе лежат 2005 монет. Двое играют в следующую игру: ходят по очереди; за ход первый может взять со стола любое нечетное число монет от 1 до 99, второй – любое четное число монет от 2 до 100. Проигрывает тот, кто не сможет сделать ход. Кто выиграет при правильной игре?

10 класс

1. Докажите, что уравнение  x⁴– 4x³ + 12x² – 24 x +24 = 0  не имеет решений.
2. Докажите, что в ходе любого сыгранного футбольного матча был момент, когда одна из команд забила голов столько же, сколько другой осталось забить.
3. Хорда удалена от центра окружности на расстояние  h.  В каждый из двух сегментов круга, стягиваемый этой хордой, вписан квадрат так, что пара его соседних вершин лежит на хорде, а другая пара соседних вершин – на соответствующей дуге окружности. Найдите разность длин сторон квадратов.
4. Найдите многочлен с целочисленными коэффициентами, корнем которого является число √2 +√3.
5. Первый член числовой последовательности равен 1, каждый из двух следующих равен 2, каждый из трех следующих за ними равен 3 и т.д. Чему равен 2005-й член этой последовательности?

11 класс

1. Докажите, что произведение четырех последовательных целых чисел, сложенное с единицей, есть точный квадрат.
2. Решите уравнение     sin⁴4x + cos²x = 2sin4x·cos⁴x.
3. Существует ли многогранник с нечетным числом граней, каждая из которых есть многоугольник с нечетным числом сторон?
4. Докажите, что касательные к гиперболе y = 1/x образуют с осями координат треугольники одной и той же площади.
5. В каждую клетку квадратной таблицы 25 x 25 вписано произвольным образом одно из чисел 1 или -1. Под каждым столбцом пишется произведение всех чисел, стоящих в этом столбце. Справа от каждой строки пишется произведение всех чисел, стоящих в этой строке. Докажите, что сумма 50 написанных произведений не может оказаться равной нулю.

Тематика заданий школьного этапа Олимпиады 
(2009/2010 уч.г.)